摘 要：针对配电网络电容器组的配置特点，建立基于配网网损最小、满足电压-无功和单组电容器容量的优化投切数学模型，提出采用逐次线性规划算法对非线性混合整数规划优化控制模型进行求解，优化求解接近最优。

关键词：电容器组；配电网；优化控制??

　　为了减少网损、提高电压水平；考虑投资、运行和维护费用等经济因素；潮流的等式约束和电压的不等式约束，在配电网中的某些节点上安装了并联补偿电容器组。因此，并联电容器组是配电网中无功补偿的主要设备，也是配电网中的主要无功源。

　　确定并联补偿电容器组在配电网中的安装位置、组数和容量后，在实时运行过程中，可根据实时负荷变化以及系统的运行状态，对电容器组进行实时动态投切，使得实时电压不越限并且网络损耗最小，因此，研究针对配电网并联补偿电容器组的实时优化投切算法和投切策略是非常有意义的。

　　配电网中电压-无功控制的控制变量一般不包含有载调压变压器分接头、发电机机端电压、调相机的输出功率，只有并联补偿电容器组，所以，配电网中的电压-无功控制的问题主要是馈线上并联补偿电容器组的实时优化投切控制问题。由于馈线间的解耦特性，配电网电容器的实时优化投切问题又可分解成若干个单馈线上电容器的实时优化投切子问题，然后逐条馈线进行优化。

1并联补偿电容器组全局优化投切控制的数学模型

　　并联补偿电容器投切所需满足的约束条件一般包括节点电压；投运电容器额定容量和投切台数的整数解等不等式约束；潮流方程等式约束。目标函数可以分为网损最小、电量损耗最小或运行费用最小。??

2并联补偿电容器组投切控制的逐次线性规划算法

2.1非线性混合整数规划模型的线性化

　　非线性模型中电容器额定容量是整数变量，这样模型中的目标函数和约束条件都是不可微分的函数，因此，在线性化前，假设非线性混合整数规划模型中投切电容器额定容量为连续变量，然后对目标函数、等式和不等式约束逐一进行线性化处理。
需要进行线性化处理主要有：
a)状态变量，即节点电压的线性化;
b)电压不等式约束的线性化;
c)目标函数有功网损的线性化;
d)电容器优化投切非线性数学模型的线性化表示。??

2.2线性混合整数规划牛型的算法

　　线性混合整数规划模型的算法是采用传统的快速算法，并充分利用并联补偿电容器组最优化投切的非线性混合整数规划模型的特点，具体是：
a) 假设模型中的整数变量为连续变量，对模型逐次进行线性化；
b) 采用传统的线性规划模型的算法；
c) 对所求得的连续变量解进行归整运算，求得最终的整数解。

　　求解线性规划问题的常用方法有两种：原始单纯法和对偶单纯法。当所要求解的线性规划问题的约束数目较少，而变量较多时，采用原始单纯法比较有利，反之，应采用对偶单纯形法。对线性规划模型而言，约束数目远大于变量总数，因此宜采用对偶单纯形法。??

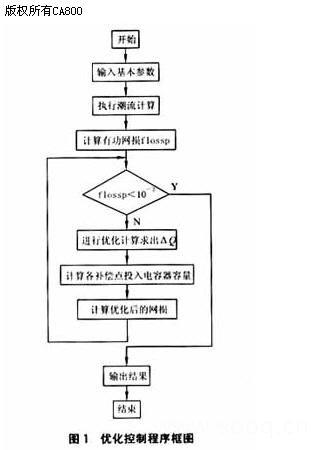
2.3优化控制程序

　　优化控制程序可见图1。框图中潮流及优化计算程序皆可利用现成的实用化程序。在用线性化模型逼近非线性化模型时，迭代计算性能对步长及初值很敏感，所以应注意选取，一般可考虑以单组电容器容量和就地无功平衡点为迭代。??

3算例

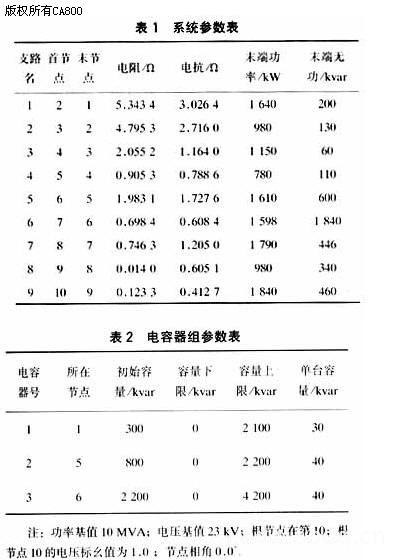
　　利用文章中所提的逐次线性规划算法，对一具有10个节点的典型放射性配电网络进行了测试计算，系统的基本参数见表1，电容器组参数见表2。?オ?

　　从以上计算结果可知：系统在最大负荷情况下，如果所有配置的电容器组均不投入时，配网网损为783.78 kW，网损率为5.96%，系统最低电压的标幺值为0.837 5，在电压下限约束0.900的条件下，应用逐次线性规划算法计算，结果得出节点1、节点5、节点6需分别投入840 kvar，1 960kvar，1 960kvar的无功功率，此时网损为689.63 kW，网损率为5.28%，最低电压的标幺值为0.886 5。比较电容器投切前后，系统的电能质量有了较大的提高，网损水平也有明显的下降。??

4结束语

　　电容器组实时投切控制模型是一个非线性混合整数规划模型，因直接求解该模型非常困难，笔者提出采用逐次线性规划算法对非线性规划模型进行求解。在求解过程中，假设整数变量为连续变量，将非线性模型线性化后求解从初值向最优解靠近的增量，通过逐次的线性化逼近非线性规划模型的最优解。在每次迭代中，还要考虑变量的整数约束，即电容器组投入容量的整数约束，所以求得电容器组投切容量的浮点解后要进行归整处理。