一些运算放大器(运放)具有感性开环输出阻抗,稳定这一类运放可能比阻性输出阻抗的运算放大器更为复杂。最常用的技术之一是使用"断开环路"方法,这涉及到断开闭环电路的反馈环路和查看环路增益以确定相位裕度。一种鲜为人知的方法是使用不需要断开环路的闭环输出阻抗。在本文中,我将讨论如何使用闭环输出阻抗来稳定带阻性或感性开环输出阻抗的运算放大器。
等式1计算闭环输出阻抗Zout,它取决于开环输出阻抗Zo,开环增益Aol,和反馈系数B。方程1表明,随着Aol的减小,Zout增加:
Zout = Zo/(1 + Aol*B) (1)
闭环输出阻抗可以是阻性、感性和双感性的,这取决于开环输出阻抗在运算放大器中的设计。对于带阻性开环输出阻抗的运算放大器,闭环输出阻抗是阻性的,并且因Aol的减小而随频率增加。当Aol减小时,闭环输出阻抗变为感性。对于带感性开环输出阻抗的运算放大器,闭环输出阻抗将具有双感性。
图1显示了运算放大器闭环输出阻抗的两个示例。左边是阻性开环输出阻抗;右边是开环输出阻抗中的感性区域。对于左侧的阻性开环输出阻抗,注意到在大约10 Hz上, Zout随频率增加,并表现为一个16.4?H的电感。右边的感性开环输出阻抗示例有三个区域:容性、阻性和感性。这使得闭环输出阻抗分别为阻性、双感性和感性。
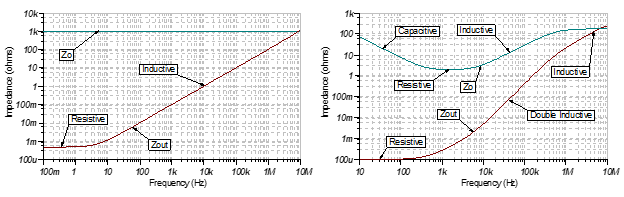
图1: 阻性Zo,阻性和感性Zout(左);带感性区域的Zo,带双感性的Zout(右)
带电阻性开环输出阻抗的运算放大器
图2显示了一个具有阻性开环输出阻抗的运算放大器驱动容性负载。
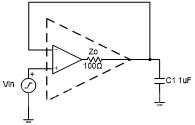
图2:驱动容性负载的阻性开环输出阻抗
图3显示了一个1μF电容的阻抗(Zc)、闭环输出阻抗(Zout)和等效闭环输出阻抗(Zeq)。可以看到,等效阻抗在大约40 kHz时(此时Zout的感性区域与容负载相交)具有谐振频率。此共振频率会引起运算放大器输出振荡,从而导致不稳定。
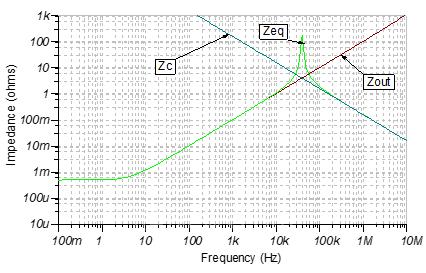
图3:1-μF电容阻抗、闭环输出阻抗和等效闭环输出阻抗
图4显示了运算放大器输出上由谐振频率引起的大量过冲。运算放大器的输出在40 kHz左右振荡。
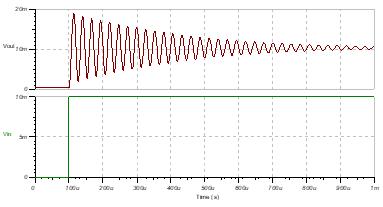
图4:输出上的大量过冲
R>2*sqrt(L/C) (2)
如前所述,Zout显示为一个16.4μH的电感。对于一个1μF的容性负载,必须使用8Ω或更大的隔离电阻来稳定电路。图5显示了带有隔离电阻的原理图。
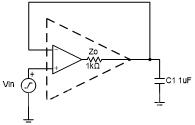
图5:带隔离电阻的原理图
图6显示了带隔离电阻的等效闭环输出阻抗(Zeq)。注意到谐振峰被消除了。
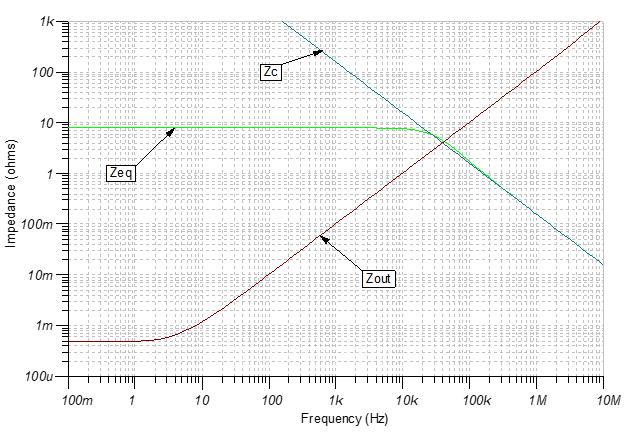
图6:带隔离电阻的等效闭环输出阻抗
图7显示,大量过冲已被添加的8Ω隔离电阻所消除。
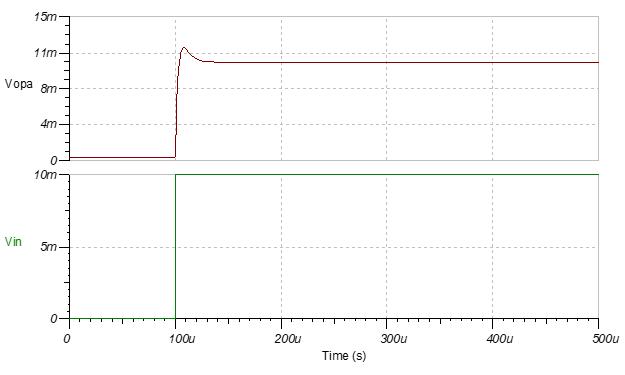
图7:使用一个8Ω隔离电阻之后的过冲
带感性开环输出阻抗的运算放大器
有些运算放大器在开环输出阻抗中有一个感性区域。这使得闭环输出阻抗变为双感性,让容性负载难以稳定。图8显示了使用一个带感性开环输出阻抗的运放的1-μF电容阻抗(Zc)、闭环输出阻抗(Zout)和等效闭环输出阻抗(Zeq)。再次注意,在约120 kHz处存在峰值,在此处,双感性闭环输出阻抗与容性负载阻抗会相互作用,从而导致不稳定性。
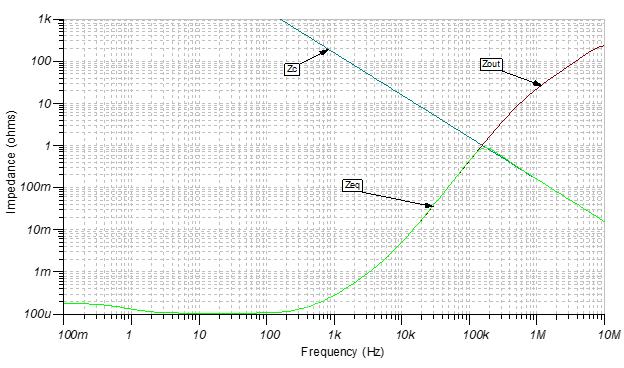
图8:1-μF电容阻抗、闭环输出阻抗和等效闭环输出阻抗
图9显示了运算放大器输出上由Zeq峰值引起的大量过冲。运算放大器的输出在120 kHz左右振荡。
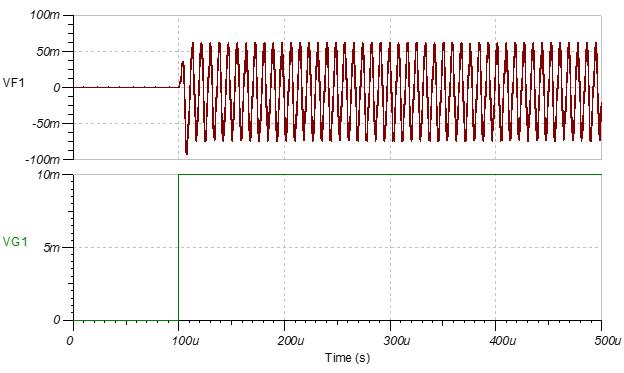
图9:输出上的大量过冲
为了纠正这种不稳定性,可以在反馈环路中添加一个电阻来改变开环输出阻抗,从而消除闭环输出阻抗中的双感性区域。这简化了隔离电阻的计算以稳定运算放大器。图10显示了反馈环路中添加的用于改变开环输出阻抗的电阻。
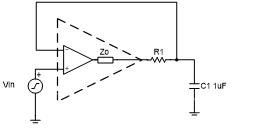
图10:反馈环路中电阻的原理图
图11显示,通过在反馈环路中添加一个100Ω的电阻,可以消除开环输出阻抗中的大部分感性区域。现在,修改后的闭环输出阻抗在10Hz以上显示为一个2.32 ?H电感。
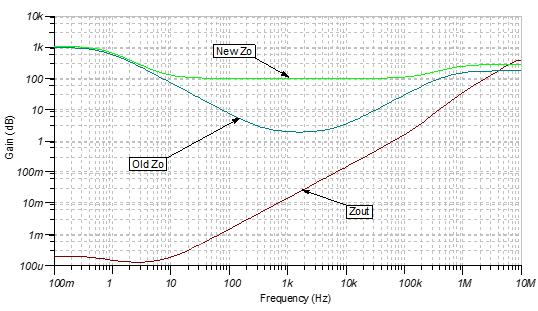
图11:修改后的开环和闭环输出阻抗
由于开环输出阻抗现在大多是阻性的,所以可以采用与使用阻性开环输出阻抗稳定运算放大器相同的方法。添加一个3Ω的隔离电阻可以稳定电路。图12显示了使用100Ω电阻修改开环输出阻抗和3Ω隔离电阻的稳定电路。
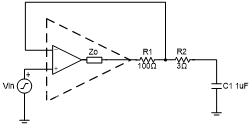
图12:带反馈电阻和隔离电阻的稳定电路的原理图
图13显示了通过向电路中添加两个电阻来消除大量过冲和回响。
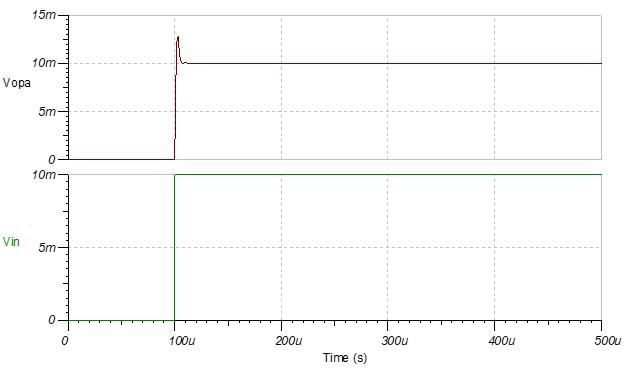
图13:反馈环路中串联一个电阻并外加一个隔离电阻之后的过冲
结论
稳定一个带感性开环输出阻抗的运放,要比稳定一个带阻性开环输出阻抗的运放复杂得多。与"断开环路"方法相比,使用闭环输出阻抗来稳定运算放大器会增加额外的好处,使您能够判断是否需要修改开环输出阻抗。在反馈环路中添加一个电阻简化了稳定带感性开环输出阻抗的运放的设计过程。
与TI高精度实验室上的运算放大器视频系列中讨论的方法相比,此方法显著降低了稳定运算放大器所需的隔离电阻值。所以下次当你发现很难稳定运算放大器时,可以考虑使用本文讨论的方法,看看在添加隔离电阻之前,是否需要修改开环输出阻抗。
参考文献
1. "基于Zout的负载电感放大器稳定性问题的闭环分析。"德州仪器应用报告SLYA029,2017年10月。







































































 京公网安备 11011202001138号
京公网安备 11011202001138号
